Assim como uma distribuição de dados pode ser simétrica, mais alongada para a esquerda ou para a direita, ela também pode ser mais alongada ou mais achatada, e para descobrir o grau de achatamento ou alongamento de uma distribuição (a concentração dos dados), é utilizado a medida de curtose, a qual pode ser classificada em:
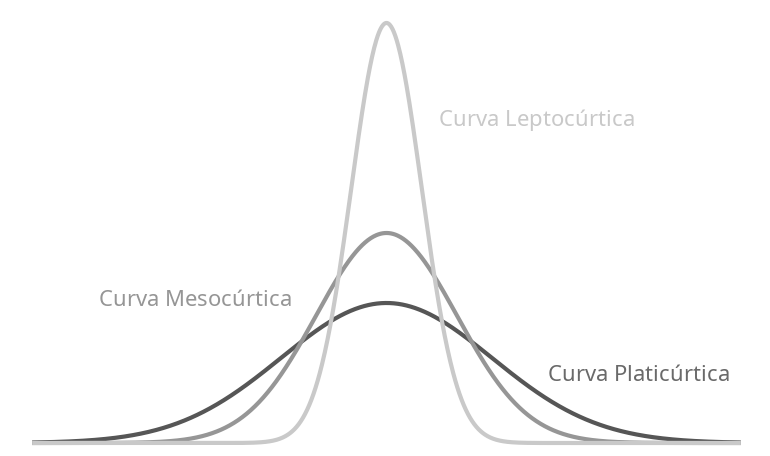
- Curva platicúrtica: apresenta o topo mais achatado que a curva normal.
- Curva Mesocúrtica: apresenta o mesmo grau de achatamento da curva normal.
- Curva Leptocúrtica: apresenta o topo mais alto, mais alongado que a curva normal.
Existe mais de uma maneira para medir o grau de achatamento de uma curva de distribuição de frequências, os principais são os coeficiente de curtose de Fisher e Pearson:
Fórmula do coeficiente de curtose de Fisher:
$$\large k = \left(\frac{\sum_{i=1}^{n} (x_{i} – \bar{x})^4}{(n-1) \cdot s⁴}\right) – 3$$
Sendo:
- $k$: coeficiente de curtose
- $\bar{x}$ ou m: média da distribuição
- $s$: desvio-padrão
- $n$: total de elementos da distribuição
Python :
k = sum(list(map(lambda x: ((x - m)**4) / ((n - 1) * s**4), values))) - 3Julia :
k = sum((values .- m).^4) / ((n - 1) * s^4) - 31ª Variação da Fórmula do coeficiente de curtose de Fisher:
$$\scriptsize k = \dfrac{n^{2} \cdot (n+1) \cdot \dfrac{\sum_{i=1}^{n}(x_{i}-\bar{x})^4}{n}}{(n-1)\cdot(n-2)\cdot(n-3)\cdot s^4} -3 \dfrac{(n-1)^2}{(n-2)\cdot(n-3)}$$
Python :
k = ((n**2 * (n+1) * (sum(list(map(lambda x: (x - m)**4, values)))/n)) / ((n-1)*(n-2)*(n-3)*s**4)) - 3 * (n-1)**2 / ((n-2)*(n-3))Julia :
k = ((n^2*(n+1) * (sum((values .- m).^4)/n)) / ((n-1)*(n-2)*(n-3)*s^4)) - 3 * ((n-1)^2 / ((n-2)*(n-3)))2ª Variação da Fórmula do coeficiente de curtose de Fisher:
Fórmula utilizada no Excel / Calc
$$\scriptsize k = { \dfrac{n \cdot (n+1)}{(n-1) \cdot (n-2) \cdot (n-3)} \cdot \sum_{i=1}^{n}\left(\dfrac{x_{i} – \bar{x}}{s}\right)^4 } – \dfrac{3 \cdot (n-1)^2}{(n-2) \cdot (n-3)}$$
Python :
k = (((n*(n+1)) / ((n-1)*(n-2)*(n-3))) * sum(list(map(lambda x: ((x - m) / s)**4, values)))) - ((3*(n-1)**2)/((n-2)*(n-3)))Julia :
k = (((n*(n+1))/((n-1)*(n-2)*(n-3))) * sum(((values .-m) ./s).^4) - ((3*(n-1)^2)/((n-2)*(n-3))))Libs:
Se for uma distribuição populacional, usa-se somente o $N$, ao invés de $(n – 1)$.
Há casos onde é usado a variância no lugar do desvio-padrão.
Classificação das curvas de distribuição pelo coeficiente de Fischer:
• se o valor de k < 0 → distribuição platicúrtica
• se o valor de k = 0 → distribuição mesocúrtica
• se o valor de k > 0 → distribuição leptocúrtica
Exemplos
Python
""" Calculando a curtose de uma série de dados não agrupados """
lista = [1, 3, 6, 10]
# média aritmética
m = sum(lista) / len(lista)
# desvio padrão
s = (sum(list(map(lambda x: ((x - m)**2), lista))) / (len(lista) - 1))**0.5
# número de elementos da série de dados
n = len(lista)
# Fórmula do Coeficiente de Fisher
k = sum(list(map(lambda x: ((x - m)**4) / ((n - 1) * s**4), lista))) - 3
print(f'Coeficiente de Fisher: {k}')Julia
""" Cálculo da curtose de uma série de dados não agrupados """
values = [1, 3, 6, 10]
# média aritmética
m = sum(values) / length(values)
# desvio padrão
s = sum(((values .- m).^2) / (length(values)-1))^0.5
# número de elementos da série de dados
n = length(values)
# Fórmula do Coeficiente de Fisher
k = sum((values .- m).^4) / ((n - 1) * s^4) - 3
println("Coeficiente de Fisher: $(k)")Python
""" Calculando a curtose de uma série de dados com intervalos de classe """
dicio ={'59.0 - 61.5':3,'61.5 - 64.0':5,'64.0 - 66.5':5,'66.5 - 69.0':7,
'69.0 - 71.5':9,'71.5 - 74.0':11,'74.0 - 76.5':8,'76.5 - 79.0':7,
'79.0 - 81.5':5,'81.5 - 84.0':6,'84.0 - 86.5':4}
# lista com o ponto médio dos intervalos de classe
pm = list(map(lambda x: (float(x.split(' - ')[0]) + float(x.split(' - ')[1])) / 2, dicio.keys()))
# lista com as frequências de cada elemento
freq = list(dicio.values())
# média aritmética
m = sum(list(map(lambda x, f: (x * f), pm, freq))) / (sum(freq))
# desvio padrão
s = (sum(list(map(lambda x, f: ((x - m)**2) * f, pm, freq))) / (sum(freq) - 1))**0.5
# número de elementos da série de dados
n = sum(freq)
# Fórmula do Coeficiente de Fisher
k = sum(list(map(lambda x, f: ((x - m)**4) * f / ((n - 1) * s**4), pm, freq))) - 3
print(f'Coeficiente de Fisher: {k}')Julia
""" Cálculo da curtose de uma série de dados com intervalos de classe """
dicionario = Dict("59.0 - 61.5"=>3,"61.5 - 64.0"=>5,"64.0 - 66.5"=>5,"66.5 - 69.0"=>7,"69.0 - 71.5"=>9,"71.5 - 74.0"=>11, "74.0 - 76.5"=>8,"76.5 - 79.0"=>7,"79.0 - 81.5"=>5,"81.5 - 84.0"=>6,"84.0 - 86.5"=>4)
# Vetor de valores com o ponto médio dos intervalos de classe
pm_freq_pairs = [(parse(Float64, split(interval, " - ")[1]) + parse(Float64, split(interval, " - ")[2])) / 2 => freq for (interval, freq) in dicionario]
# vetor com os pontos médios
pm = [pair[1] for pair in pm_freq_pairs]
# vetor com as frequências
freq = [pair[2] for pair in pm_freq_pairs]
# Média ponderada
m = sum(pm .* freq) / sum(freq)
# desvio padrão
s = (sum(((pm .- m).^2) .* freq) / (sum(freq) - 1))^0.5
# Número de elementos total
n = sum(freq)
# Fórmula do Coeficiente de Fisher
k = sum(((pm .- m).^4) .* freq / ((n - 1) * s^4)) - 3
println("Coeficiente de Fisher: $(k)")Python
'''Utilizando a 2ª variação da fórmula, utilizada no Excel / Calc'''
dicio ={'59.0 - 61.5':3,'61.5 - 64.0':5,'64.0 - 66.5':5,'66.5 - 69.0':7,
'69.0 - 71.5':9,'71.5 - 74.0':11,'74.0 - 76.5':8,'76.5 - 79.0':7,
'79.0 - 81.5':5,'81.5 - 84.0':6,'84.0 - 86.5':4}
# Ponto médio de cada intervalo de classe
pm = list(map(lambda x: (float(x.split(' - ')[0]) + float(x.split(' - ')[1])) / 2, dicio.keys()))
# Frequência de cada elemento da série de dados
freq = list(dicio.values())
# Criando uma lista com todos os pontos médios e suas repetições
lista = [pm[n] for n in range(len(pm)) for _ in range(freq[n])]
# média aritmética
m = sum(lista) / len(lista)
# número de elementos da série de dados
n = len(lista)
# desvio padrão
s = (sum(list(map(lambda x: (x - m)**2, lista))) / (n - 1))**0.5
f = sum(list(map(lambda x: ((x - m) / s)**4, lista)))
# Fórmula do Excel
k = (((n*(n+1)) / ((n-1)*(n-2)*(n-3))) * sum(list(map(lambda x: ((x - m) / s)**4, lista)))) - ((3*(n-1)**2)/((n-2)*(n-3)))
print(k)Julia
""" Agora, utilizando a 2ª variação da fórmula, utilizada no Excel / Calc """
dicionario = Dict("59.0 - 61.5"=>3,"61.5 - 64.0"=>5,"64.0 - 66.5"=>5,"66.5 - 69.0"=>7,"69.0 - 71.5"=>9,"71.5 - 74.0"=>11, "74.0 - 76.5"=>8,"76.5 - 79.0"=>7,"79.0 - 81.5"=>5,"81.5 - 84.0"=>6,"84.0 - 86.5"=>4)
# Vetor de valores com o ponto médio dos intervalos de classe
pm_freq_pairs = [(parse(Float64, split(interval, " - ")[1]) + parse(Float64, split(interval, " - ")[2])) / 2 => freq for (interval, freq) in dicionario]
# vetor com os pontos médios
pm = [pair[1] for pair in pm_freq_pairs]
# vetor com as frequências
freq = [pair[2] for pair in pm_freq_pairs]
# Criando um vetor com todos os pontos médios e suas repetições
values = [p for (p, f) in zip(pm, freq) for _ in 1:f]
# Média aritimética
m = sum(values) / length(values)
# Número de elementos total
n = length(values)
# desvio padrão
s = (sum((values .- m).^2) / (n - 1))^0.5
# Fórmula do Excel
k = (((n*(n+1))/((n-1)*(n-2)*(n-3))) * sum(((values .-m) ./s).^4) - ((3*(n-1)^2)/((n-2)*(n-3))))
println(k)Python
''' Utilizando a biblioteca Scipy '''
import scipy.stats as sc
dicio ={'59.0 - 61.5':3,'61.5 - 64.0':5,'64.0 - 66.5':5,'66.5 - 69.0':7,
'69.0 - 71.5':9,'71.5 - 74.0':11,'74.0 - 76.5':8,'76.5 - 79.0':7,
'79.0 - 81.5':5,'81.5 - 84.0':6,'84.0 - 86.5':4}
pm = list(map(lambda x: (float(x.split(' - ')[0]) + float(x.split(' - ')[1])) / 2, dicio.keys()))
freq = list(dicio.values())
lista = [pm[n] for n in range(len(pm)) for _ in range(freq[n])]
k = sc.kurtosis(lista)
print(k)Julia
""" Utilizando a biblioteca StatsBase """
using StatsBase
dicionario = Dict("59.0 - 61.5"=>3,"61.5 - 64.0"=>5,"64.0 - 66.5"=>5,"66.5 - 69.0"=>7,"69.0 - 71.5"=>9,"71.5 - 74.0"=>11, "74.0 - 76.5"=>8,"76.5 - 79.0"=>7,"79.0 - 81.5"=>5,"81.5 - 84.0"=>6,"84.0 - 86.5"=>4)
# Vetor de valores com o ponto médio dos intervalos de classe
pm_freq_pairs = [(parse(Float64, split(interval, " - ")[1]) + parse(Float64, split(interval, " - ")[2])) / 2 => freq for (interval, freq) in dicionario]
# vetor com os pontos médios
pm = [pair[1] for pair in pm_freq_pairs]
# vetor com as frequências
freq = [pair[2] for pair in pm_freq_pairs]
# Criando um vetor com todos os pontos médios e suas repetições
values = [p for (p, f) in zip(pm, freq) for _ in 1:f]
k = kurtosis(values)
println(k)Fórmula do coeficiente de curtose de Pearson:
$$\large k = \frac{\sum_{i=1}^{n} (x_{i} – \bar{x})^4}{(n-1) \cdot s⁴}$$
Sendo:
- $k$: coeficiente de curtose
- $\bar{x}$: média da distribuição
- $s$: desvio-padrão
- $n$: total de elementos da distribuição
Python :
k = sum(list(map(lambda x: ((x - m)**4) / ((n - 1) * s**4), lista)))Julia :
k = sum(((values .- m).^4) / ((n-1) * s^4))Se for uma distribuição populacional usa-se somente o $N$ ao invés de $(n – 1)$
Há casos onde é usado a variância no lugar do desvio-padrão.
Classificação das curvas de distribuição pelo coeficiente de Pearson:
• se o valor de k < 3 → distribuição platicúrtica
• se o valor de k = 3 → distribuição mesocúrtica
• se o valor de k > 3 → distribuição leptocúrtica
Exemplos
Python
''' Calculando a curtose de uma série de dados '''
lista = [1, 3, 6, 10]
# média aritmética
m = sum(lista) / len(lista)
# desvio padrão
s = (sum(list(map(lambda x: ((x - m)**2), lista))) / (len(lista) - 1))**0.5
# número de elementos da série de dados
n = len(lista)
# Fórmula do Coeficiente de Pearson
k = sum(list(map(lambda x: ((x - m)**4) / ((n - 1) * s**4), lista)))
print(f'Coeficiente de Pearson: {k}')Julia
""" Cálculo da curtose de uma série de dados """
values = [1, 3, 6, 10]
# média aritmética
m = sum(values) / length(values)
# desvio padrão
s = sum(((values .- m).^2) / (length(values)-1))^0.5
# número de elementos da série de dados
n = length(values)
# Fórmula do Coeficiente de Pearson
k = sum(((values .- m).^4) / ((n-1) * s^4))
println("Coeficiente de Pearson: $(k)")Python
''' Calculando a curtose de uma série de dados com intervalos de classe '''
dicio ={'59.0 - 61.5':3,'61.5 - 64.0':5,'64.0 - 66.5':5,'66.5 - 69.0':7,
'69.0 - 71.5':9,'71.5 - 74.0':11,'74.0 - 76.5':8,'76.5 - 79.0':7,
'79.0 - 81.5':5,'81.5 - 84.0':6,'84.0 - 86.5':4}
# lista com o ponto médio dos intervalos de classe
pm = list(map(lambda x: (float(x.split(' - ')[0]) + float(x.split(' - ')[1])) / 2, dicio.keys()))
# lista com as frequências de cada elemento
freq = list(dicio.values())
# média aritmética
m = sum(list(map(lambda x, f: (x * f), pm, freq))) / (sum(freq))
# desvio padrão
s = (sum(list(map(lambda x, f: ((x - m)**2) * f, pm, freq))) / (sum(freq) - 1))**0.5
# número de elementos da série de dados
n = sum(freq)
# Fórmula do Coeficiente de Pearson
k = sum(list(map(lambda x, f: ((x - m)**4) * f / ((n - 1) * s**4), pm, freq)))
print(f'Coeficiente de Pearson: {k}')Julia
""" Cálculo da curtose de uma série de dados com intervalos de classe """
dicionario = Dict("59.0 - 61.5"=>3,"61.5 - 64.0"=>5,"64.0 - 66.5"=>5,"66.5 - 69.0"=>7,"69.0 - 71.5"=>9,"71.5 - 74.0"=>11, "74.0 - 76.5"=>8,"76.5 - 79.0"=>7,"79.0 - 81.5"=>5,"81.5 - 84.0"=>6,"84.0 - 86.5"=>4)
# Vetor de valores com o ponto médio dos intervalos de classe
pm_freq_pairs = [(parse(Float64, split(interval, " - ")[1]) + parse(Float64, split(interval, " - ")[2])) / 2 => freq for (interval, freq) in dicionario]
# vetor com os pontos médios
pm = [pair[1] for pair in pm_freq_pairs]
# vetor com as frequências
freq = [pair[2] for pair in pm_freq_pairs]
# Média ponderada
m = sum(pm .* freq) / sum(freq)
# desvio padrão
s = (sum(((pm .- m).^2) .* freq) / (sum(freq) - 1))^0.5
# Número de elementos total
n = sum(freq)
# Fórmula do Coeficiente de Pearson
k = sum(((pm .- m).^4) .* freq / ((n - 1) * s^4))
println("Coeficiente de Pearson: $(k)")Fórmula do coeficiente de curtose de Bowley (coeficiente percentílico):
$$\large k = \frac{Q_{3} – Q{1}}{2 \cdot (P_{90}-P_{10})}$$
Sendo:
- k: coeficiente percentílico de curtose
- Q3: valor do terceiro quartil
- Q1: valor do primeiro quartil
- P90: valor do 90º percentil
- P10: valor do 10º percentil
Python / Julia :
k = (Q3 - Q1) / (2 * (P90 - P10))Classificação das curvas de distribuição pelo coeficiente de Bowley:
• se o valor de k > 0,263 → distribuição platicúrtica
• se o valor de k = 0,263 → distribuição mesocúrtica
• se o valor de k < 0,263 → distribuição leptocúrtica
O coeficiente percentílico se difere dos demais, pois seu intuito não é quantificar a forma das caudas e o pico de distribuição, mas sim, medir o como os dados se espalham (spread, espalhamento) a partir do centro da distribuição, ao redor da mediana e entre os quartis, isso o torna menos sensível à valores extremos e mais robusto em relação a outliers.
Exemplos
Python
''' Calculando a curtose de uma série de dados com intervalos de classe '''
dicio ={'59.0 - 61.5':3,'61.5 - 64.0':5,'64.0 - 66.5':5,'66.5 - 69.0':7,
'69.0 - 71.5':9,'71.5 - 74.0':11,'74.0 - 76.5':8,'76.5 - 79.0':7,
'79.0 - 81.5':5,'81.5 - 84.0':6,'84.0 - 86.5':4}
# Frequência acumulada
fa = list(map(lambda x: sum(list(dicio.values())[: x + 1]), range(len(dicio.values()))))
# separatrizes a se encontrar (quartis 1 e 3 / percentis 10 e 90)
sep = []
# Para encontrar os valores utiliza-se a fórmula das separatrizes com um laço 'for'
for n in [1, 3, 10, 90]:
if n in [1, 3]:
# posição dos quartis e percentis procurados
pn = (n * sum(list(dicio.values()))) / 4
else:
# posição dos quartis e percentis procurados
pn = (n * sum(list(dicio.values()))) / 100
# operações para encontrar o intervalo de classe que está a separatriz procurada
num = list(filter(lambda x: x >= pn, fa))[0]
interval = list(dicio.keys())[fa.index(list(filter(lambda x: x == num, fa))[0])]
# limite inferior da classe do quartil ou do percentil
li = float(interval.split(' - ')[0])
# amplitude da classe
h = float(interval.split(' - ')[1]) - float(interval.split(' - ')[0])
# frequência acumulada anterior à classe que se está verificando os dados
m = list(filter(lambda x: x < pn, fa))[-1]
# frequência simples da classe que se está verificando os dados
fm = dicio.get(interval)
# Fórmula para encontrar as separatrizes
Q = li + ((h * (pn - m))/fm)
sep.append(Q)
Q1, Q3, P10, P90 = sep
# Fórmula da Curtose de Bowley
k = (Q3 - Q1) / (2 * (P90 - P10))
print(f'Coeficiente Percentílico de Curtose: {k}')Julia
dicionario = Dict("59.0 - 61.5"=>3,"61.5 - 64.0"=>5,"64.0 - 66.5"=>5,"66.5 - 69.0"=>7,"69.0 - 71.5"=>9,"71.5 - 74.0"=>11, "74.0 - 76.5"=>8,"76.5 - 79.0"=>7,"79.0 - 81.5"=>5,"81.5 - 84.0"=>6,"84.0 - 86.5"=>4)
dicio = [pair for pair in sort(collect(dicionario))]
intervalos = [pair[1] for pair in dicio]
freq = [pair[2] for pair in dicio]
fa = cumsum(freq)
sep = []
for n in [1, 3, 10, 90]
if n in [1, 3]
# posição dos quartis e percentis procurados
pn = (n * sum(freq)) / 4
else
# posição dos quartis e percentis procurados
pn = (n * sum(freq)) / 100
end
# operações para encontrar o intervalo de classe que está a separatriz procurada
num = filter(x -> x >= pn, fa)[1]
interval = intervalos[findfirst(x -> x == num, fa)]
# limite inferior da classe do quartil ou do percentil
li = parse(Float64, split(interval, " - ")[1])
# amplitude da classe
h = parse(Float64, split(interval, " - ")[2]) - parse(Float64, split(interval, " - ")[1])
# frequência acumulada anterior à classe que se está verificando os dados
m = filter(x -> x < pn, fa)[end]
# frequência simples da classe que se está verificando os dados
fm = freq[findfirst(x -> x == interval, intervalos)]
# Fórmula para encontrar as separatrizes
Q = li + ((h * (pn - m)) / fm)
push!(sep, Q)
end
Q1, Q3, P10, P90 = sep
k = (Q3 - Q1) / (2 * (P90 - P10))Python
''' Utilizando a biblioteca STATISTICS '''
import statistics as st
dicio ={'59.0 - 61.5':3,'61.5 - 64.0':5,'64.0 - 66.5':5,'66.5 - 69.0':7,
'69.0 - 71.5':9,'71.5 - 74.0':11,'74.0 - 76.5':8,'76.5 - 79.0':7,
'79.0 - 81.5':5,'81.5 - 84.0':6,'84.0 - 86.5':4}
# Ponto médio de cada intervalo de classe
pm = list(map(lambda x: (float(x.split(' - ')[0]) + float(x.split(' - ')[1])) / 2, dicio.keys()))
# Frequência de cada elemento da série de dados
freq = list(dicio.values())
# Criando uma lista com todos os pontos médios e suas repetições
lista = [pm[n] for n in range(len(pm)) for _ in range(freq[n])]
Q1 = st.quantiles(lista, n=4, method='inclusive')[0]
Q3 = st.quantiles(lista, n=4, method='inclusive')[2]
P10 = st.quantiles(lista, n=100, method='inclusive')[9]
P90 = st.quantiles(lista, n=100, method='inclusive')[89]
k = (Q3 - Q1) / (2 * (P90 - P10))
print(k)''' Agora, utilizando a biblioteca NUMPY '''
import numpy as np
dicio ={'59.0 - 61.5':3,'61.5 - 64.0':5,'64.0 - 66.5':5,'66.5 - 69.0':7,
'69.0 - 71.5':9,'71.5 - 74.0':11,'74.0 - 76.5':8,'76.5 - 79.0':7,
'79.0 - 81.5':5,'81.5 - 84.0':6,'84.0 - 86.5':4}
# Ponto médio de cada intervalo de classe
pm = list(map(lambda x: (float(x.split(' - ')[0]) + float(x.split(' - ')[1])) / 2, dicio.keys()))
# Frequência de cada elemento da série de dados
freq = list(dicio.values())
# Criando uma lista com todos os pontos médios e suas repetições
lista = [pm[n] for n in range(len(pm)) for _ in range(freq[n])]
Q1 = np.quantile(lista, 0.25, method='weibull')
Q3 = np.quantile(lista, 0.75, method='weibull')
P10 = np.percentile(lista, 10, method='weibull')
P90 = np.percentile(lista, 90, method='weibull')
k = (Q3 - Q1) / (2 * (P90 - P10))
print(k)Julia
""" Utilizando a biblioteca Statistics """
using Statistics
dicionario = Dict("59.0 - 61.5"=>3,"61.5 - 64.0"=>5,"64.0 - 66.5"=>5,"66.5 - 69.0"=>7,"69.0 - 71.5"=>9,"71.5 - 74.0"=>11, "74.0 - 76.5"=>8,"76.5 - 79.0"=>7,"79.0 - 81.5"=>5,"81.5 - 84.0"=>6,"84.0 - 86.5"=>4)
# Vetor de valores com o ponto médio dos intervalos de classe
pm_freq_pairs = [(parse(Float64, split(interval, " - ")[1]) + parse(Float64, split(interval, " - ")[2])) / 2 => freq for (interval, freq) in dicionario]
# vetor com os pontos médios
pm = [pair[1] for pair in pm_freq_pairs]
# vetor com as frequências
freq = [pair[2] for pair in pm_freq_pairs]
# Criando um vetor com todos os pontos médios e suas repetições
values = [p for (p, f) in zip(pm, freq) for _ in 1:f]
Q1 = quantile(values, 0.25)
Q3 = quantile(values, 0.75)
P10 = quantile(values, 0.10)
P90 = quantile(values, 0.90)
k = (Q3 - Q1) / (2 * (P90 - P10))
println(k)""" Agora, utilizando a biblioteca StatsBase """
using StatsBase
dicionario = Dict("59.0 - 61.5"=>3,"61.5 - 64.0"=>5,"64.0 - 66.5"=>5,"66.5 - 69.0"=>7,"69.0 - 71.5"=>9,"71.5 - 74.0"=>11, "74.0 - 76.5"=>8,"76.5 - 79.0"=>7,"79.0 - 81.5"=>5,"81.5 - 84.0"=>6,"84.0 - 86.5"=>4)
# Vetor de valores com o ponto médio dos intervalos de classe
pm_freq_pairs = [(parse(Float64, split(interval, " - ")[1]) + parse(Float64, split(interval, " - ")[2])) / 2 => freq for (interval, freq) in dicionario]
# vetor com os pontos médios
pm = [pair[1] for pair in pm_freq_pairs]
# vetor com as frequências
freq = [pair[2] for pair in pm_freq_pairs]
# Criando um vetor com todos os pontos médios e suas repetições
values = [p for (p, f) in zip(pm, freq) for _ in 1:f]
Q1 = nquantile(values, 4)[2]
Q3 = nquantile(values, 4)[4]
P10 = nquantile(values, 100)[11]
P90 = nquantile(values, 100)[91]
k = (Q3 - Q1) / (2 * (P90 - P10))
Deixe um comentário